Выявление корреляции между микроконверсиями и определение зависимости между действиями посетителей сайта с офлайн продажами поможет повысить эффективность вашей контекстной рекламы.
Итак, в первой части этой статьи я уже рассказала вам о коэффициенте корреляции Пирсона, его применении и ограничениях в использовании, а именно — обязательное наличие линейной зависимости между переменными. Зачастую такую зависимость сложно найти, так как, например, проведение распродаж может резко увеличить количество достижений целей и как следствие — появление выбросов на графиках. Но есть другой коэффициент корреляции, который не нуждается в линейных зависимостях.
Коэффициент корреляции Спирмена
Это такой коэффициент корреляции, для расчета которого не требуется предположений о характере распределений признаков в генеральной совокупности. Предварительно сравниваемые величины переводятся в ранговую шкалу и уже после этого рассчитывается теснота взаимосвязи между ними.
Диапазон значений коэффициента корреляции Спирмена лежит в интервале [-1;1]. Он также может быть положительным и отрицательным, характеризуя направленность связи между двумя величинами, измеренными в ранговой шкале.
Формула коэффициента Спирмена следующая:

где в числителе дроби мы видим сумму квадратов разностей между рангами от случая отсутствия связи, а n — количество строк в нашей таблице.
Интерпретация коэффициента аналогична коэффициенту Пирсона:
| Значение коэффициента корреляции r | Интерпретация |
| 0 < r ≤ 0,2 | Очень слабая корреляция |
| 0,2 < r ≤ 0,5 | Слабая корреляция |
| 0,5 < r ≤ 0,7 | Средняя корреляция |
| 0,7 < r ≤ 0,9 | Сильная корреляция |
| 0,9 < r ≤ 1 | Очень сильная корреляция |
Единой формулы для расчета коэффициента Спирмена в MS Excel нет, поэтому будем разбираться с ним на нашем примере по кусочкам.
Разбираемся
Итак, построив точечные графики между диапазонами данных при прочтении прошлой статьи (ссылка на файл SpreadSheets тут), вы обнаружили отсутствие линейной зависимости между элементами. Значит, пришло время посчитать ранги.
Что такое ранг числа? Это его величина относительно других значений в списке чисел. Определить его можно с помощью формулы (задаем само число, ранг которого определяем, массив, в котором оно содержится и порядок):
=РАНГ.РВ(Число;Массив1;1)
То есть, нам необходимо создать вторую табличку (размером с исходную) и заполнить все ячейки соответствующей формулой, проставляя в нее число, ранг которого ищем, диапазон и порядок, равный 1.
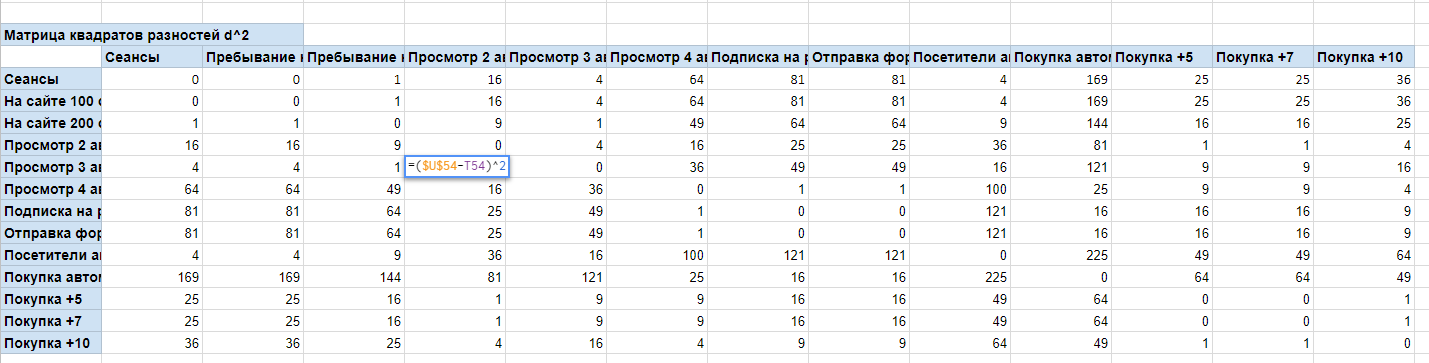
Мы нашли ранги всех чисел. Но формула содержит сумму квадратов разностей между рангами, поэтому под каждым столбцом матрицы рангов рассчитываем сумму элементов.
А теперь составляем матрицу квадратов разностей между рангами. Ее размер зависит от количества столбцов в исходной таблице (за исключением даты). В каждую ячейку матрицы прописывается разность сумм элементов и возводится в квадрат.
По главной диагонали матрицы (из верхнего левого угла в правый нижний угол) должны получиться 0. Например, берем первую ячейку (1,1), здесь нужно расписать разность между суммой рангов по сеансам и возвести в квадрат. Сумма рангов по сеансам = 1324, поэтому подставляя в формулу, получаем (1324-1324)^2 = 0. В ячейке (2,2) аналогичная ситуация и т.д.
При подсчете других элементов матрицы используется та же формула. Например, для ячейки на пересечении целей «Просмотр 2 авто» и «Просмотр 3 авто» подставляем суммы рангов в формулы и получаем (1320-1322)^2 = 4.
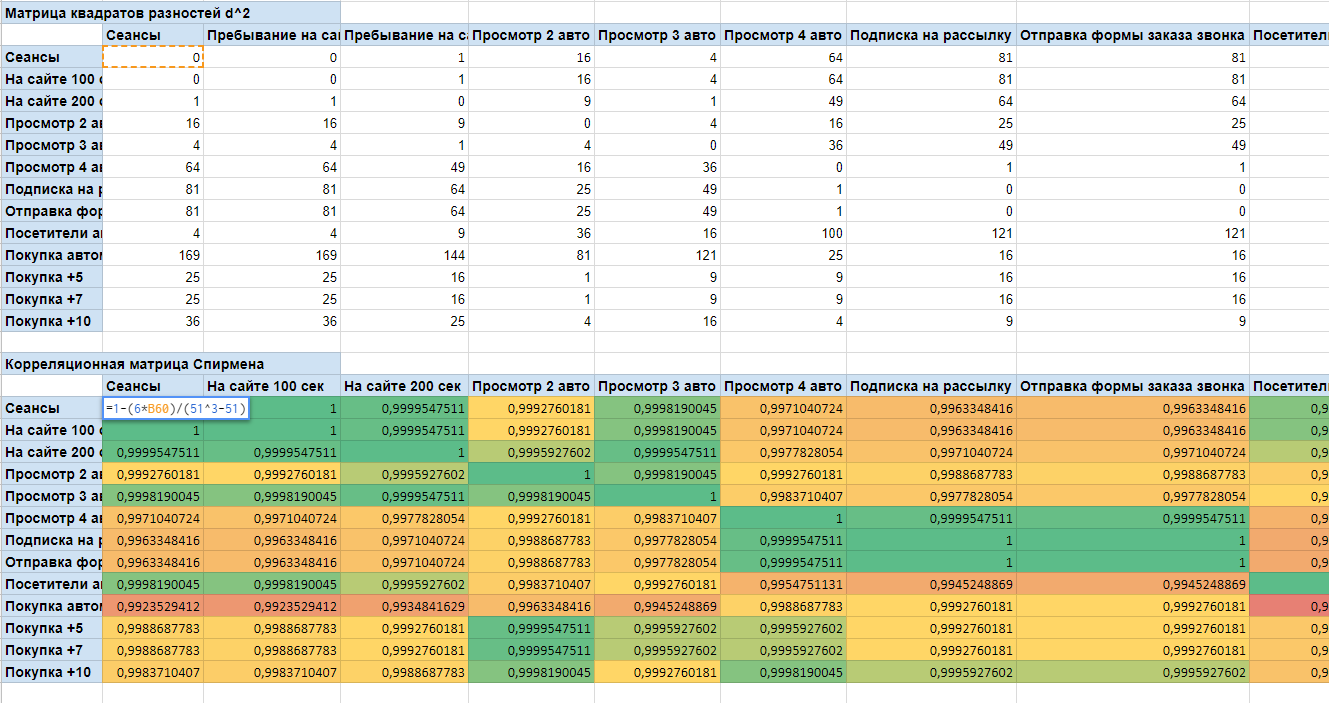
Наконец, мы можем приступить к формированию нашей корреляционной матрицы. Действуем далее по нашей формуле. Видим неизвестный нам n, чтобы узнать его — посчитайте количество строк в исходной таблице. У меня получилось 51.
И теперь, используя матрицу квадратов разностей составляем такого же размера корреляционную. Напоминаю, что в корреляционной матрице по главной диагонали должны получиться 1.
Рассчитываем элемент (1,1). В формулу вместо d^2 подставляем найденный элемент (1,1) из матрицы квадратов разностей, а вместо n — количество строк всей таблицы. И так для всех остальных элементов.
Результаты
Получаем корреляционную матрицу. И также, как и в предыдущем примере, видим слабую и сильную корреляцию.
Ищем интересные связи с достижениями целей. Например, пользователи, заполнившие форму заказа обратного звонка и те, кто покупают автомобиль на 10-й день сильно коррелируют между собой. Строим точечный график между двумя диапазонами данных по нашим показателям и видим отсутствие линейной зависимости и наличие выбросов, именно то, почему мы использовали коэффициент Спирмена:

Выводы
При расчете корреляции необходимо запомнить одно важное правило:
Корреляция не означает причинность.
То, что события коррелируют между собой — не означает, что люди покупают автомобили на 10-й день только потому, что отправили заявку на обратный звонок с сайта. Это может быть случайность или влияние какой-либо третьей величины, о которой мы не знаем.
В любом случае коэффициенты корреляции дают нам полезную информацию о связи микроконверсий, с которой мы можем экспериментировать для повышения эффективности рекламных кампаний.
Ссылки:





привет! спасибо за статьи.
У меня вопрос по трактовке данных в последней таблице.
Получается, если клиент купил через 5 дней авто, то еще через два дня он купит второе?
Привет!
Фактически да, но я использовала искусственные данные, поэтому некоторые связи могут быть нелогичными. Моя основная задача — показать сам метод, а данные будет использовать каждый — свои 🙂
В таблице корреляции почти все коэффиценты ~ 0,99, то есть везде очень сильная корреляция. Где-то ошибка или так и должно быть?
Привет! Как я уже писала ниже — я использовала искусственные данные и так вышло, что их корреляция действительно высока. На реальных данных коэффициенты должны быть нормальными)