При настройке ремаркетинга необходимо указывать цели, при достижении которых реклама будет догонять пользователя в процессе его путешествия по сети, чтобы он вернулся и сделал заказ, если он когда-то прервал процесс покупки. Это могут быть цели на добавление в корзину, переход к оплате и т.д.
Но такая настройка не всегда означает, что ремаркетинг эффективен на все 100%, ведь к достижению целей могут вести другие микроконверсии, о чьих связях мы и не догадываемся. В этой статье я расскажу о применении корреляционного анализа для выявления связей между целевыми действиями пользователей для эффективной настройки вашей рекламы.
Что вообще такое корреляция?
Корреляция — это взаимозависимость двух или нескольких случайных величин, а на сколько сильна эта зависимость, показывает коэффициент корреляции.
В нашем случае коэффициент корреляции будет показывать насколько связаны микроконверсии между собой, с целевым действием пользователя и можем ли мы их использовать для настройки ремаркетинга.
Подготовка к анализу
Рассмотрим на примере. У нас есть сайт автодилера, салон которого пользуется особой популярностью. На сайте представлен каталог автомобилей для подробного ознакомления перед приездом в салон. Несколько месяцев назад были настроены цели/события в Google Analytics (для расчетов необходимы ретроспективные данные). Какие микроконверсии для этого можно использовать? Любые. Для сайта интернет магазина это могут быть добавления товаров в корзину, подписки на рассылку, звонки, переходы в корзину, непосредственно транзакции и другие необходимые вам действия. Для анализа можно взять также и офлайн продажи из CRM, что мы и сделаем в нашем примере.
На первый взгляд, изначально мы не знаем, как связаны посетители сайта и покупатели автосалона. Придут ли за покупкой автомобиля те, кто подписался на рассылку или заказал обратный звонок? Коэффициент корреляции как раз и покажет связь между такими действиями пользователей. А для более точной проверки влияния посещаемости сайта на покупку автомобиля офлайн учтем временной лаг, не все пользователи в день посещения сайта бегут в автосалон, поэтому данные по заказам сдвинем на несколько дней, например, установим столбцы со сдвигами 0, 5, 7 и 10 дней.
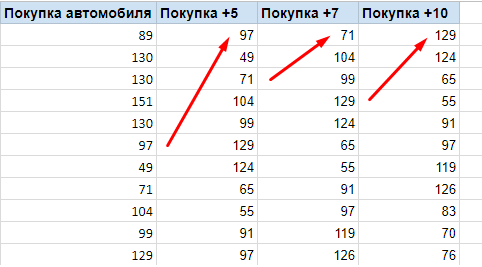
Для нашего примера берем следующие показатели и цели:
- Сеансы
- Пребывание на сайте 100 сек
- Пребывание на сайте 200 сек
- Просмотр 2 автомобилей
- Просмотр 3 автомобилей
- Просмотр 4 автомобилей
- Подписка на рассылку
- Отправка формы заказа звонка
А также выгрузка из CRM об офлайн продажах:
- Посетители автосалона
- Покупка автомобиля
- Покупка автомобиля +5
- Покупка автомобиля +7
- Покупка автомобиля +10
Как выгрузить данные по целям?
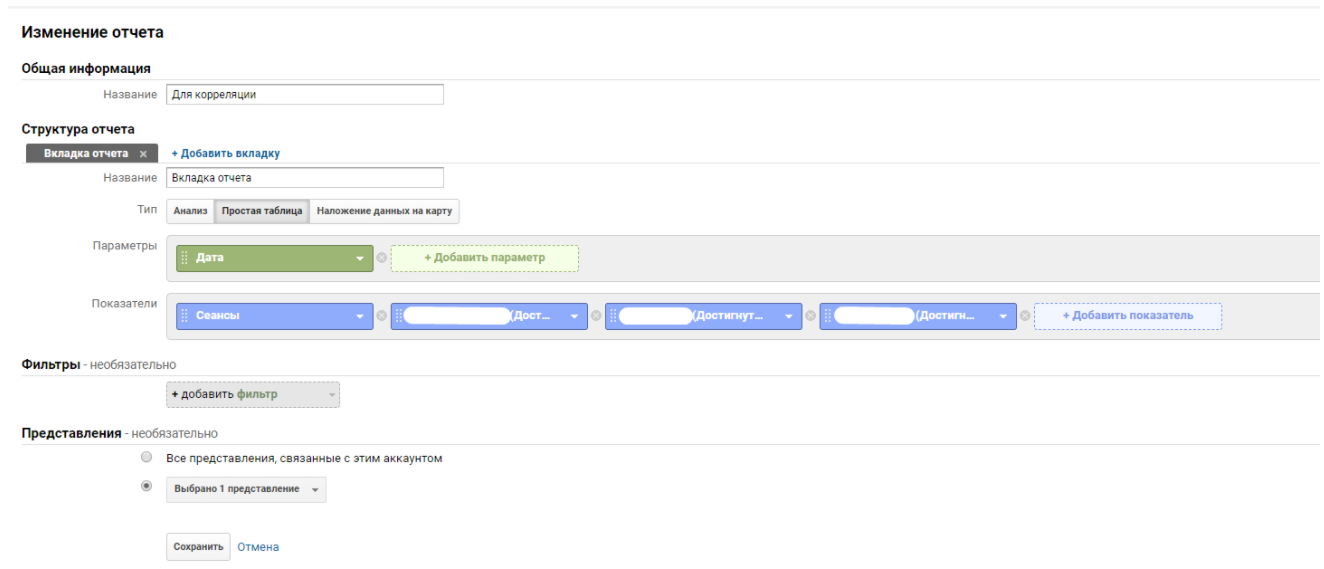
Сразу возникает логичный вопрос — как проще выгрузить данные для анализа. Я предлагаю для этого построить специальный отчет. В Google Analytics это вкладка «Специальные отчеты->Мои отчеты->Добавить отчет». Выбираем тип отчета «Простая таблица» и добавляем наши параметры и показатели. В данном случае нам понадобится Дата, Сеансы и Достигнутые переходы к целям.
Сохраняем отчет, выбираем в правом верхнем углу нужный временной диапазон и сортируем по дате (кликаем на шапку первого столбца). Также, не забудьте раскрыть все строки (максимально 5000 строк), так как Google Analytics выгружает только видимую часть таблицы.
Ну и в верхнем правом углу нажимаем «Экспортировать->EXCEL (XLSX)».
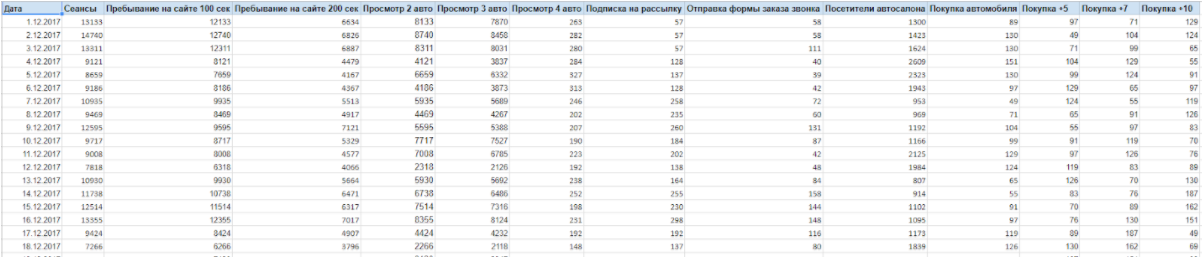
Выгруженные данные уже разбиты по столбцам, к ним добавляем столбец с офлайн продажами из CRM, если это вам необходимо, и, теперь, с данными можно работать. Вот какая табличка получилась в Spreadsheets . Тут я взяла период с 1.12.2017 по 30.01.2018 по дням.
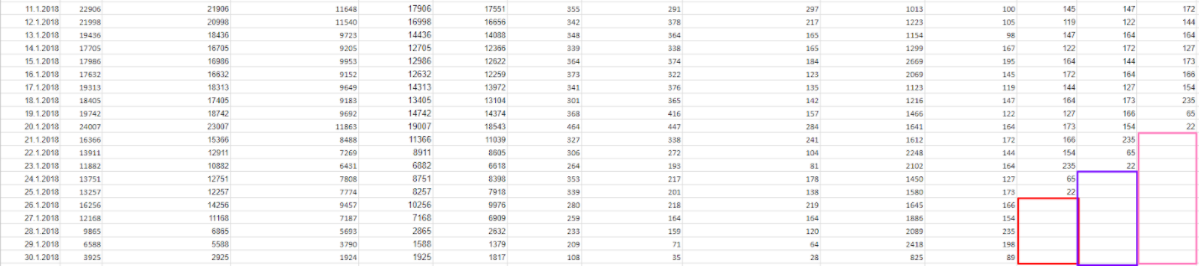
Обращаю ваше внимание, что из-за продаж автомобилей в салонах со сдвигами 5, 7 и 10 дней, данные также сдвигаются, то есть, конец таблички выглядит следующим образом:
На всякий случай прикладываю сюда ссылку на мою табличку с рассчитанной корреляционной матрицей, которая доступна здесь.
Для удобства можно удалить нижние строки таблицы, чтобы количество строк совпадало с количеством значений последнего столбца. Для анализа будем рассматривать два коэффициента корреляции — Пирсона и Спирмена. В этой части статьи я расскажу про использование первого коэффициента.
Коэффициент корреляции Пирсона
Коэффициент корреляции Пирсона характеризует существование линейной взаимосвязи между двумя величинами. Это значит, что при увеличении одной величины вторая также будет увеличиваться (при положительном коэффициенте) и уменьшаться (при отрицательном). Стоит отметить, что коэффициент Пирсона не устойчив к выбросам. Это значит, что если вы построите точечный график по данным двух столбцов и не сможете представить прямую линию, вдоль которой примерно распределены значения, то коэффициент корреляции Пирсона, скорее всего, здесь неприменим и вам потребуется другой коэффициент, о котором я расскажу во второй части статьи.
Вот пример нелинейной:
И линейной зависимости:
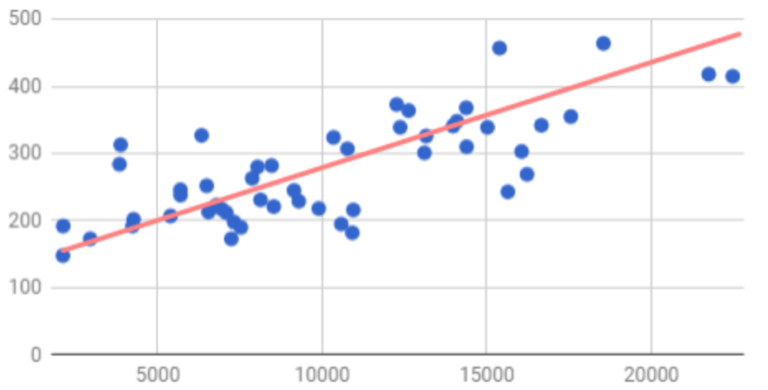
Интерпретация значений коэффициента
Значение коэффициента корреляции располагается в пределах от 0 до 1. Сила зависимости в основном интерпретируется следующим образом.
| Значение коэффициента корреляции r | Интерпретация |
| 0 < r ≤ 0,2 | Очень слабая корреляция |
| 0,2 < r ≤ 0,5 | Слабая корреляция |
| 0,5 < r ≤ 0,7 | Средняя корреляция |
| 0,7 < r ≤ 0,9 | Сильная корреляция |
| 0,9 < r ≤ 1 | Очень сильная корреляция |
Например, корреляция между посещением корзины и покупкой будет стремиться к 1, а корреляция между просмотром страницы «Вакансии» и онлайн-заказом будет не такой высокой и, скорее всего, будет близка к 0.
В MS Excel (а также в Spreadsheets) есть стандартная функция для расчета коэффициента корреляции Пирсона
=КОРРЕЛ(Массив1;Массив2)
Размер корреляционной матрицы зависит от количества столбцов в таблице (за исключением даты). Если вы выгрузили 8 показателей, то получится табличка 8х8.
В каждой ячейке матрицы прописывается функция КОРРЕЛ и значения двух массивов для соответствующей строки/столбца. По главной диагонали матрицы (из верхнего левого угла в правый нижний угол) у вас должны получиться 1, так как корреляция столбца самим с собой = 1. Например, берем первую ячейку (1,1), здесь сеансы коррелируют с сеансами, подставляем в формулу массив сеансов два раза и получаем 1. В ячейке (2,2) аналогичная ситуация и т.д.
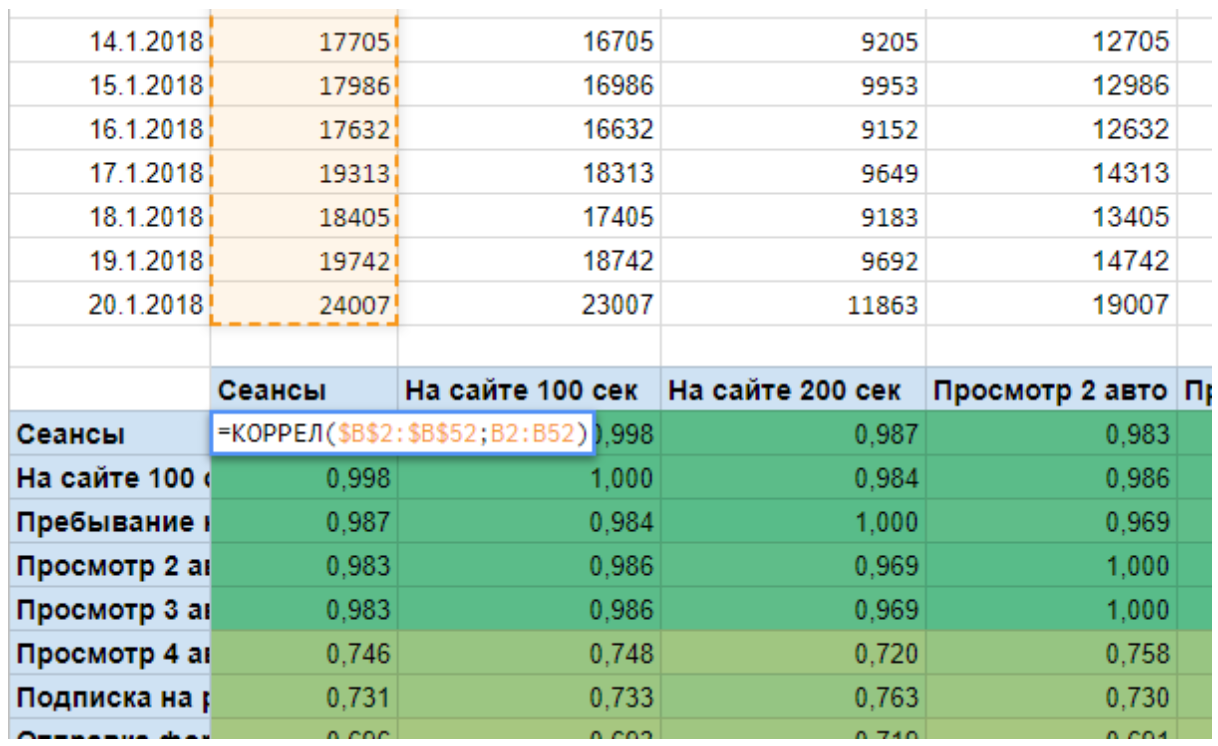
Если вы считаете корреляцию, например, как у меня для Сеансов и Количества достигнутых целей с просмотром страниц с 2-мя автомобилями, то в качестве массивов выбираете эти столбцы и значение прописываете в пересечение этих показателей.
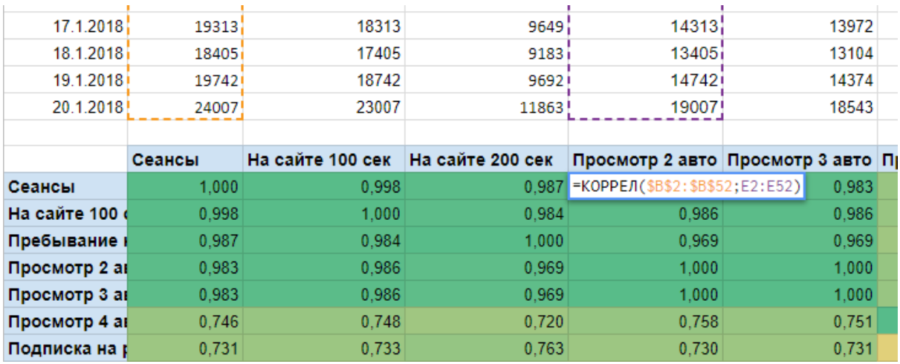
Как вы уже, наверно, догадались, достаточно заполнить половину матрицы, так как значения над главной диагональю и под ней будут будут одинаковыми. Это происходит от того, что от перестановки мест массивов в формуле коэффициент корреляции не изменится, не важно, ищете ли вы зависимость между сеансами и просмотрами 2-х авто или наоборот просмотром 2-х авто и сеансами, корреляция будет одинаковой.
К матрице желательно применить условное форматирование, чтобы было легче анализировать коэффициенты.
Результаты
В конечном итоге получаем корреляционную матрицу.
Итак, где-то видим сильную (зеленый цвет), а где-то слабую корреляцию (оранжевый, красный). Как и ожидалось, длительность пребывания на сайте сильно коррелирует с количеством просмотренных страниц с автомобилями.
Но нас интересуют цели сайта, которые могли привести к покупке в салоне. Очевидно, что коэффициент корреляции высоким не будет, но какую-то взаимосвязь увидеть сможем. Вот, например, просмотр страниц 4 автомобилей и покупка автомобиля через 5 дней имеют между собой корреляцию равную 0,653. Из таблицы выше видим, что это коэффициент корреляции средней силы, но он связан с офлайн продажами и может подсказать, какие целевые действия на сайте приводят пользователей к покупке, а, значит, мы можем определить дополнительную цель для настройки ремаркетинга. Строим точечный график между двумя диапазонами данных по нашим показателям и видим следующее:
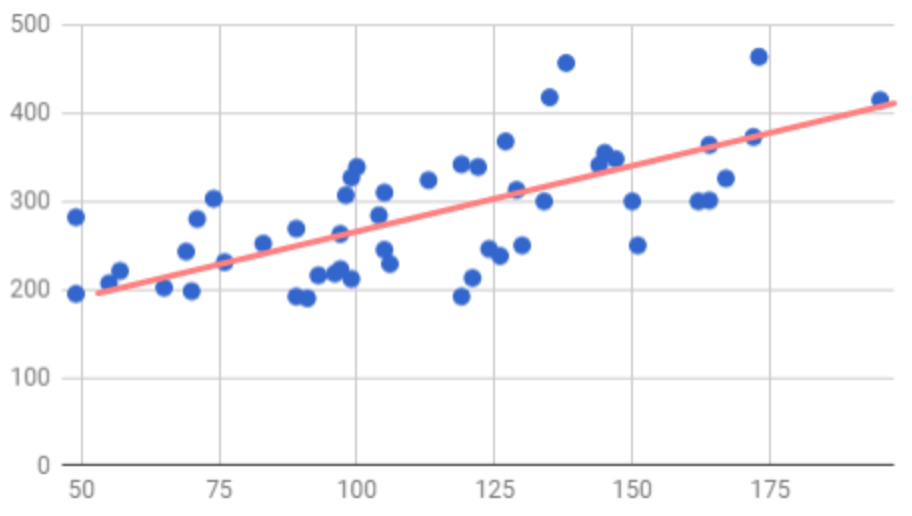
Смело можем построить прямую, вдоль которой прыгают значения, а, значит, можем говорить о линейной зависимости. Далее, можете построить другие точечные графики, чтобы убедиться в линейной зависимости между переменными и применимости коэффициента Пирсона для вашего случая.
Выводы
Уже на этом этапе можно делать выводы о связи микроконверсий и переходить к настройке ремаркетинга на новые цели, у которых была выявлена связь с офлайн или онлайн продажами.
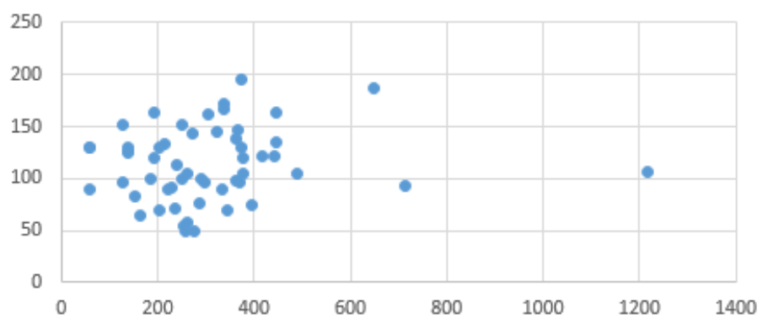
Но чаще оказывается на деле, что все не так просто и на графике видны выбросы — возможно, результаты праздников или распродаж, и уже не так легко заметить линейную зависимость, если она вообще будет.
График зависимости переменных может выглядеть следующим образом:
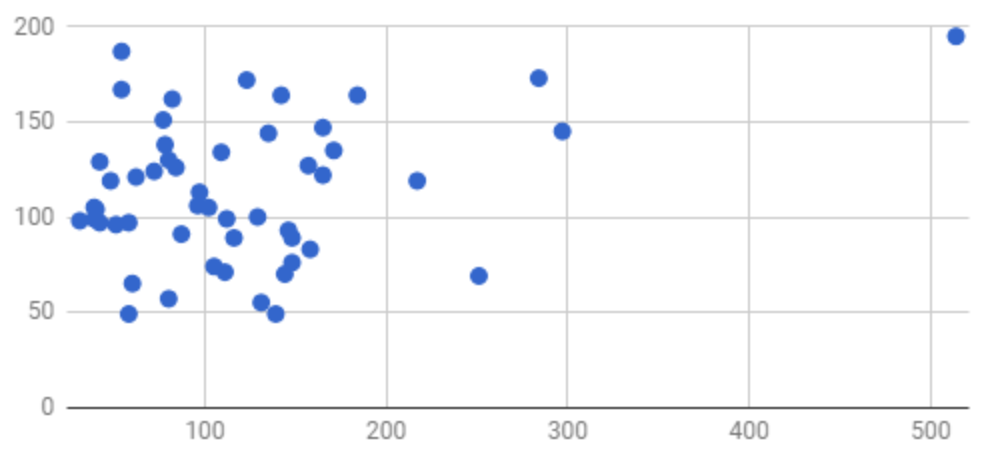
Не похоже, что график расположен вдоль прямой, к тому же видим выброс в правом верхнем углу, и, следовательно, коэффициент корреляции Пирсона в этом случае не подойдет.
Проверяя таким образом другие взаимосвязи, вы можете несколько раз столкнуться с нелинейной зависимостью между величинами. Чтобы это обойти, используют коэффициент корреляции Спирмена, о котором я расскажу в следующей статье.
Ссылки: