В прошлой статье мы уже разобрали, что такое временной ряд и функцию тренда. Теперь подробнее разберемся с терминологией и остановимся на одной из моделей временного ряда.

Из чего состоит временной ряд

Уровни временного ряда (Yt) представляют из себя сумму двух компонент:

1. Регулярную составляющую
2. Случайную составляющую

В свою очередь регулярная составляющая состоит из:

1. Тренда
2. Сезонности
3. Циклической составляющей

Однако, в модели необязательно наличие всех этих компонент сразу.

Случайная компонента отражает влияние случайных возмущений на модель, которые по отдельности имеют незначительное воздействие, но суммарно их влияние ощущается.

То есть, в общем случае временной ряд представляет из себя наличие четырех составляющих:

1. Тренд (Tt)
2. Сезонность (St)
3. Цикличность (Ct)
4. Случайные возмущения (Et)

Циклическая компонента, по сравнению с сезонностью, имеет более длительный эффект и меняется от цикла к циклу. Поэтому, ее обычно объединяют с трендом.

Виды моделей временного ряда

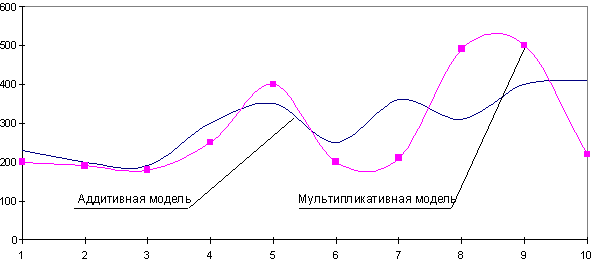
Обычно, выделяют две модели временного ряда и третью — смешанную.

1. Аддитивная модель 

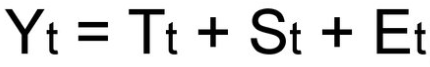
2. Мультипликативная модель  

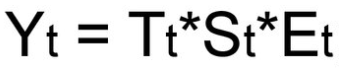
3. Смешанная модель  

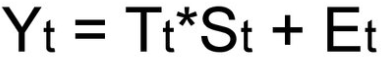
При выборе необходимой модели временного ряда смотрят на амплитуду колебаний сезонной составляющей. Если ее колебания относительно постоянны, то выбирают аддитивную модель.  То есть, амплитуда колебаний примерно одинакова:

Если  амплитуда  сезонных  колебаний  возрастает  или  уменьшается,  строят мультипликативную  модель  временного  ряда,  которая  ставит  уровни  ряда в зависимость от значений сезонной компоненты.

Построение этих моделей сводится к расчету тренда (Tt), сезонности (St) и случайных возмущений (Et) для каждого уровня ряда (Yt).

Алгоритм построения модели

1. Выравниваем ряд с помощью скользящей средней, то есть сглаживаем ряд и отфильтровываем высокочастотные колебания.
2. Рассчитываем значение сезонной компоненты St.
3. Рассчитываем значения Tt с использованием полученного уравнения тренда.
4. Используя полученные значения St и Tt, находим прогнозные значения уровней временного ряда.
5. Оцениваем качество модели.

Реализация на практике

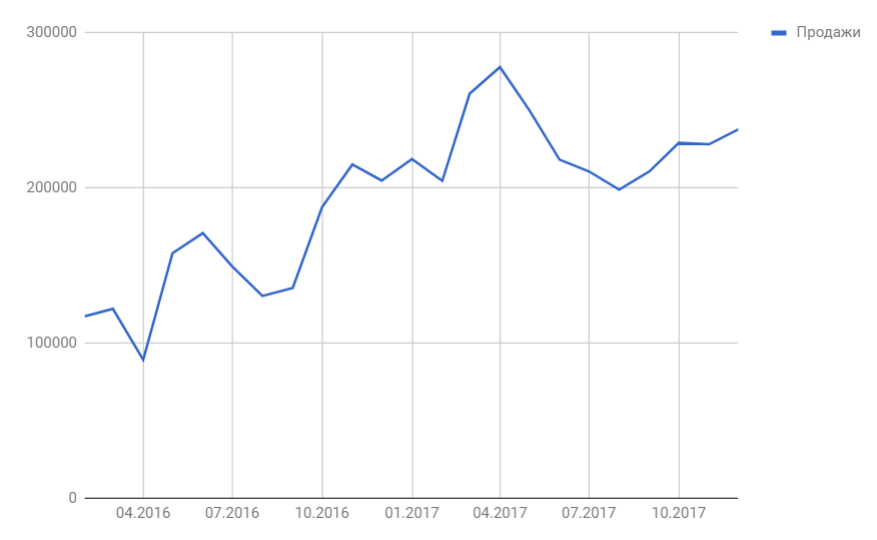
Итак, мы имеем на руках данные о продажах за 2016 и 2017 год и хотим спрогнозировать продажи на 2018 год.

Шаг 1

Следуя нашему алгоритму, мы должны сгладить временной ряд. Воспользуемся методом скользящей средней. Видим, что  в каждом году есть большие пики (май-июнь 2016 и апрель 2017), поэтому возьмем период сглаживания пошире, например, месячную динамику, т.е. 12 месяцев.

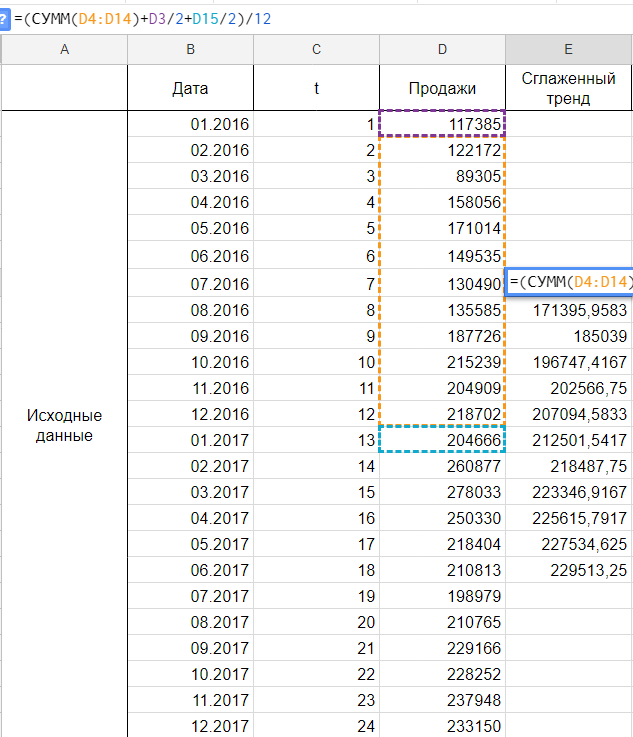
Удобнее брать период сглаживания в виде нечетного числа, тогда формула для расчета уровней сглаженного ряда:

yi — фактическое значение i-го уровня ряда,

yt — значение скользящей средней в момент времени t,

2p+1 — длина интервала сглаживания.

Но так как мы решили использовать месячную динамику в виде четного числа 12, то данная формула нам не подойдет и мы воспользуемся этой:

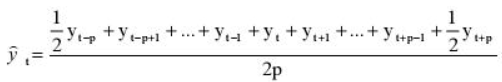
Иными словами, мы учитываем половины от крайних уровней ряда в диапазоне, в остальном формула не претерпела больше никаких изменений. Вот ее точный вид для нашей задачи:

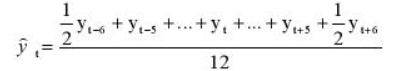
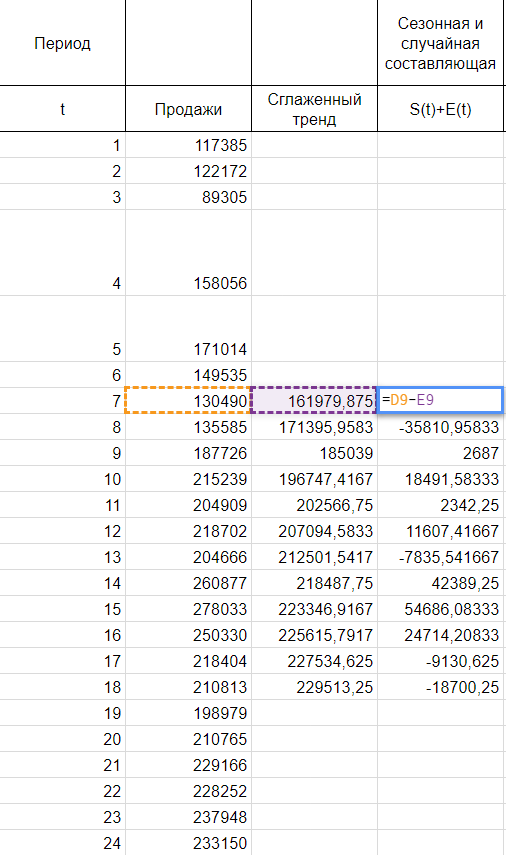
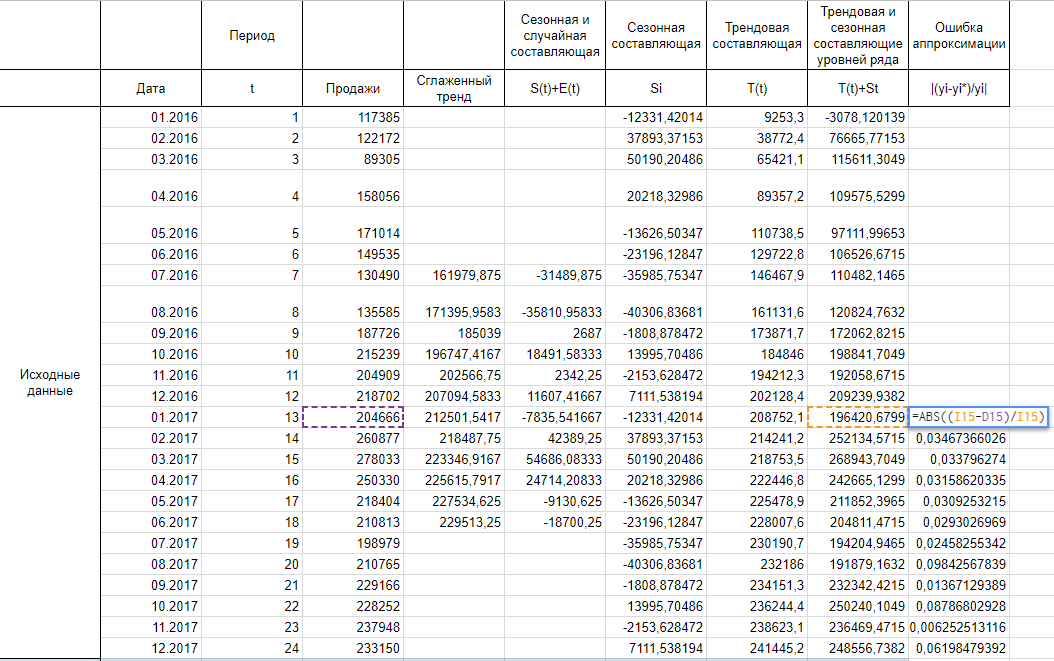
Сглаживаем наши уровни ряда и растягиваем формулу вниз:

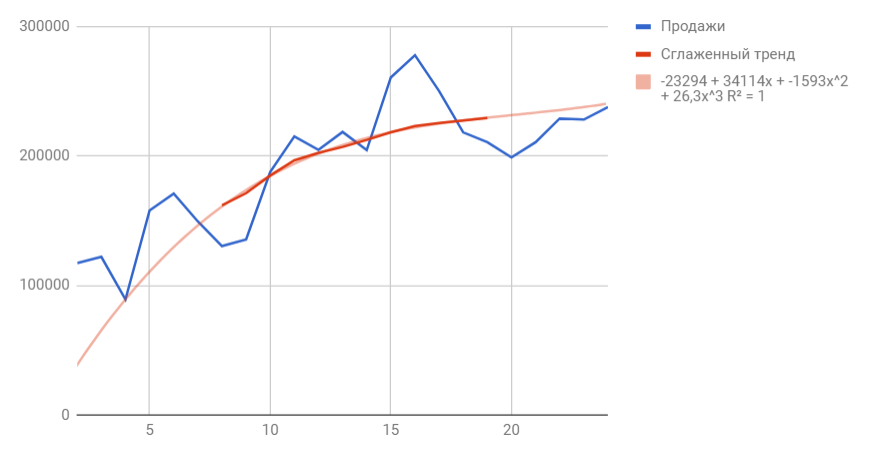
Сразу можем построить график из известных значений уровня продаж и их сглаженной. Выведем ее уравнение и значение коэффициента детерминации R^2:

В качестве сглаженной я выбрала полином третьей степени, так как он лучше всего описывал уровни временного ряда и имел наибольший R^2.

Шаг 2

Так как мы рассматриваем аддитивную модель вида: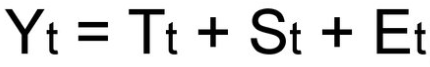 

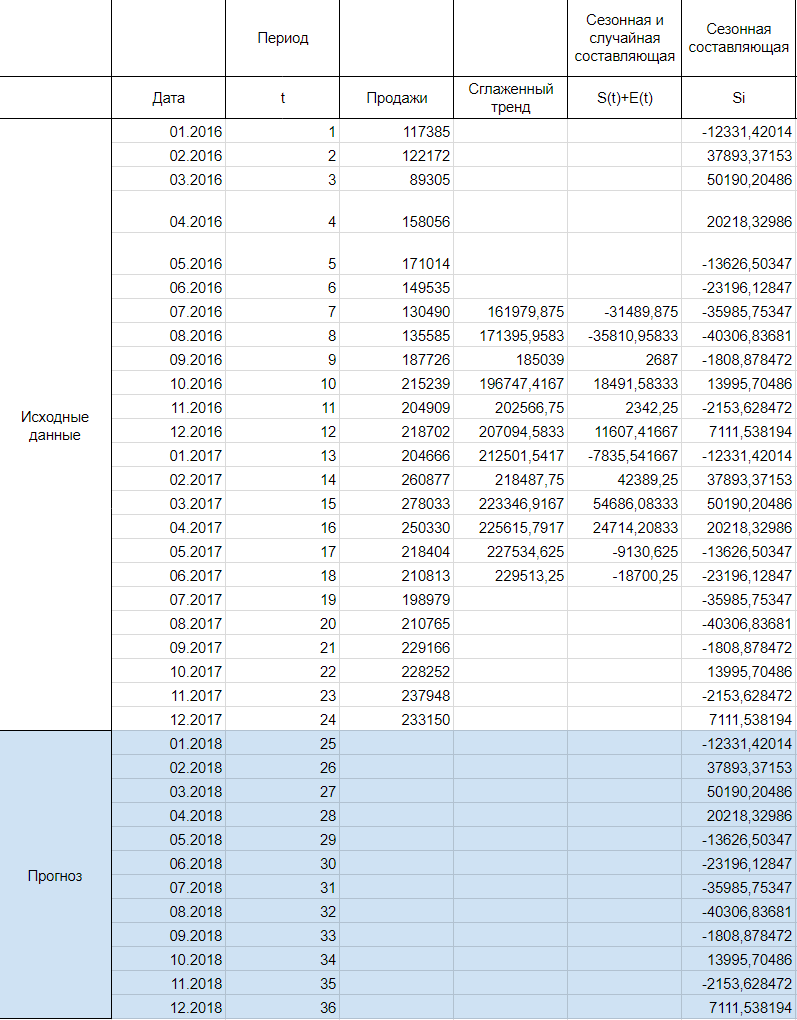
Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и значениями скользящей средней St+Et = Yt-Tt, так как Yt и Tt мы уже знаем.

Используем оценки сезонной компоненты (St+Et) для расчета значений сезонной компоненты St. Для этого найдем средние за каждый интервал (по всем годам) оценки сезонной компоненты St.

Средняя оценка сезонной компоненты находится как сумма по столбцу, деленная на количество заполненных строк в этом столбце. В нашем случае оценки сезонной составляющей расположились в строках без пересечений, поэтому сумма по столбцам состоит из одиночных значений, следовательно и среднее будет таким же. Если бы мы располагали периодом побольше, например с 2015, у нас бы добавилась еще одна строка и мы смогли бы полноценно найти среднее, поделив сумму на 2.

В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем интервалам должна быть равна нулю. Поэтому найдя значение случайной составляющей, поделив сумму средних оценок сезонной составляющей на 12, мы вычитаем ее значение из каждой средней оценки и получаем скорректированную сезонную компоненту, St.

Далее, заполняем нашу таблицу значениями сезонной составляющей дублируя ряд каждые 12 месяцев, то есть три раза:

Шаг 3

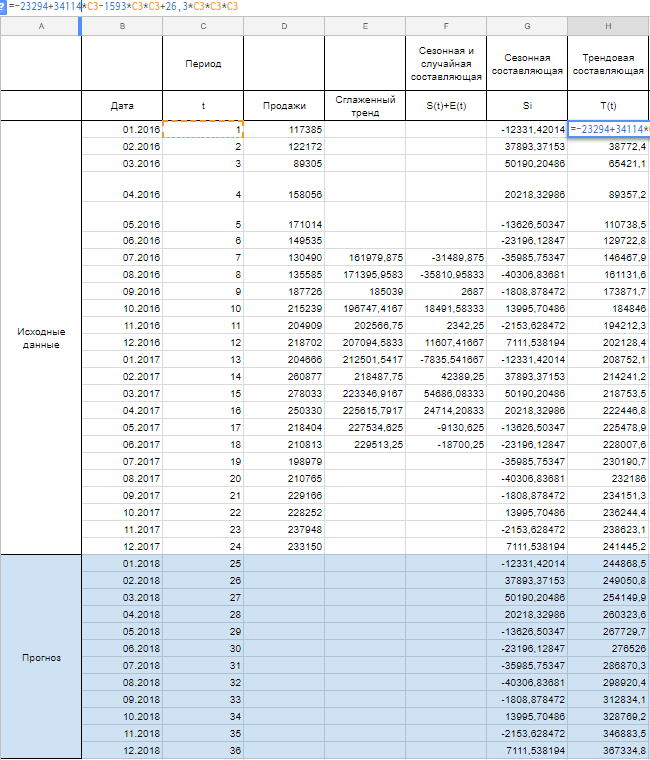
Теперь рассчитываем значения уровня тренда T(t) по тому уравнению, которое мы получили при построении сглаженного тренда на первом шаге.

T(t) = -23294+34114*t-1593*t^2+26,3*t^3

Вместо t используем значения из столбца Период из соответствующей строки.

Шаг 4

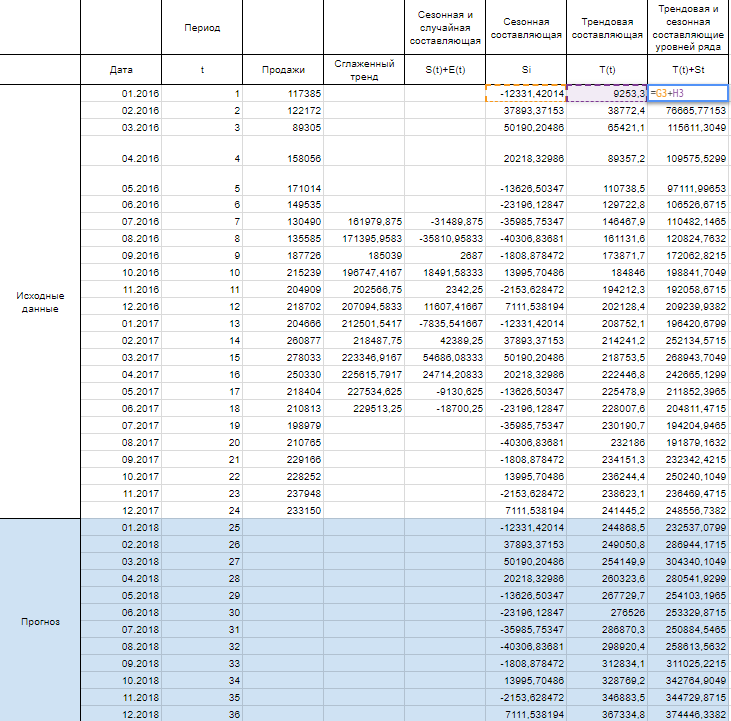
Имея рассчитанные значения S(t) и T(t) мы можем рассчитать прогнозные значения уровней ряда Y(t). Для этого накладываем уровни сезонности на тренд.

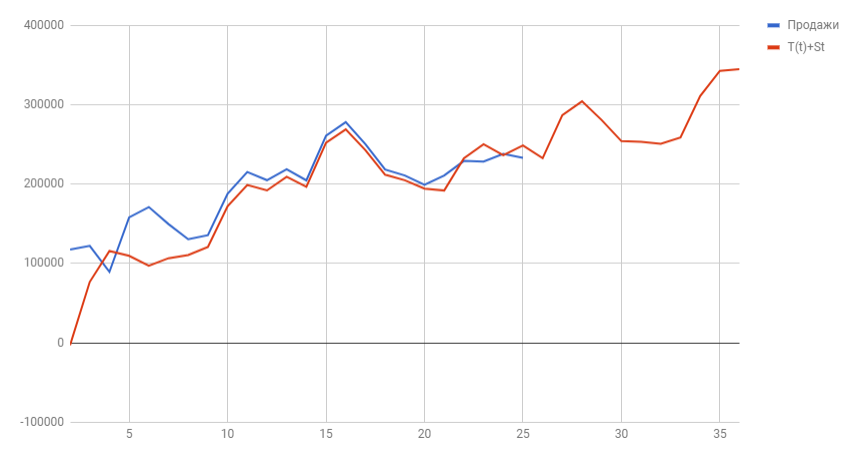
Теперь построим график известных значений Y(t) и спрогнозированных за 2018 год.

Вот мы и нашли спрогнозированные значения уровней продаж на 2018 год. Значения отражают возрастающую тенденцию и сезонные пики. Конечно, эти данные не дают 100% точности, ведь существует множество внешних воздействий, которые могут изменить направление тренда, поэтому к прогнозным значениям обычно строят доверительный интервал, это такой коридор, внутри которого могут колебаться прогнозные значения с заданной вероятностью (чаще всего выбирают 95%). Но об этом я расскажу в следующей статье.

Шаг 5

Осталось оценить точность модели. Для этого будем использовать среднюю ошибку аппроксимации, которая поможет рассчитать ошибку в относительном выражении. Иными словами, это среднее отклонение расчетных значений от фактических, которое вычисляется по формуле:

yi — спрогнозированные уровни ряда,

yi* — фактические уровни ряда,

n — количество складываемых элементов.

Модель может считаться адекватной, если:

Итак, рассчитываем ошибку аппроксимации для нашего случая. Так как в основе нашего тренда лежит полином третьей степени, прогнозные значения начинают хорошо повторять фактические значения к концу 2016 года, думаю, я думаю, поэтому корректнее было бы рассчитать ошибку аппроксимации для значений 2017 года.

Сложив весь столбец с ошибками аппроксимации и поделив на 12, получаем среднюю ошибку аппроксимации 4,13%. Это значение меньше 15% и можем сделать вывод об адекватности модели.

Не забывайте, что прогнозы не бывают точными на 100%. Любые неожиданные внешние воздействия могут развернуть значения уровней ряда в неизвестном направлении 🙂

Полезные ссылки:

• Ссылка на пример Google Sheets
• Построение функции тренда в Excel. Быстрый прогноз без учета сезонности
• Бывшев В.А. Эконометрика

• Об авторе
• Свежие записи

Екатерина Шипова

Магистр прикладной математики и информатики, веб-аналитик. Сертифицированный специалист Google Аnalytics и Яндекс.Метрика.

• Прогнозирование продаж в Excel с учетом сезонности - 27.06.2018
• Построение функции тренда в Excel. Быстрый прогноз без учета сезонности - 05.06.2018
• Когортный анализ. Сколько пользователей к вам вернулось? - 24.05.2018